Chapter 01
The History of Digital Cash
Digital currencies are some of the most interesting and mind-boggling technological and economic phenomena to have been enabled by the Internet. What initially started as a theoretical issue in computer science bothering a handful of geeks has turned into a catalyst for paradigm shifts beyond pieces of code. In cryptocurrencies, the right sequences of ones and zeros have evolved past mathematical expressions of informational bits as they have acquired a strong societal dimension. Ultimately, they have become political statements.
While economists like to argue about the nature of cryptocurrencies and whether they are money or not, the truth is that cryptocurrencies now signify much more than just money. They are a new class of assets. The consequences of technology, especially when it comes to our economy and technology, is beyond our comprehension.
While nowadays most people have at least heard of Bitcoin, there is still very little written, about the multidimensional paradigm shifts that cryptocurrencies will deliver. And while for most people, cryptocurrencies are only about Bitcoin, Bitcoin is not, by any means, the first nor the only digital currency ever conceived. There have been many attempts to design and implement electronic currencies to varying levels of success.
Since the invention of the modern web, computer wizards have sought the electronic version of money. As we advanced in connecting machines around the globe to allow seamless transfer of digital data, the invention of digital cash was all but inevitable. All of the digital currency ideas began being cobbled together as papers, some developed further into code, and even fewer translated into actionable companies or projects. What they all shared in common was that they built upon the work of the great cryptographers and computer scientists of the 20th century. To comprehend cryptocurrencies fully, it is crucial to understand the origin and circumstances in which their technological backbone was created.
Public Key Infrastructure
The 1970s gave the world numerous innovations, but the creation of public-key cryptography is perhaps one of the most valuable, yet underappreciated. Before that, cryptography in general had been predominantly the domain of military and intelligence services securing their own communication. Likewise, research activities in this area were mostly limited to three-letter agencies, either those falling under direct government supervision, like NSA, or private enterprises with appropriate licenses such as IBM. The public had little access to the knowledge created, in large part, by their taxes. A significant milestone was the inception and subsequent publication of *public-key cryptography* by Martin Hellman, Whitfield Diffie, and Ralph Merkle. The results of their work would translate into a massive spike in the public’s awareness of cryptography and would set the groundwork for the vanguards of the Cypherpunk movement in the decades to come.
For thousands of years, humankind has made efforts to secure and protect communication in the battle between codemakers and codebreakers. While information has always been an increasingly valuable commodity, some information is more valuable than others. The risk of having a secret communication intercepted by enemies was a great threat. In fact, kings, queens, and entire nations have often risen and fallen based on their handle of secret communication.
According to Herodotus, known as “The Father of History,', who chronicled the Greco-Persian Wars, it was the art of secret communication that saved Greece from being conquered by the despotic leader of Persia, Xerxes. Had they not been notified by one of their fellow countrymen living in Persia about Xerxes' plans to attack Greece, the country would not have been capable of resisting one the largest armies ever assembled. Greeks received the secret messages on wooden tablets covered in wax, cajoling them into arming themselves and preparing for an attack. Had the message not been hidden*,* the Persian guards would have likely intercepted the communication and thwarted the element of surprise.
The art of secret communication and hidden messages evolved into a field we today call steganography. Unlike steganography, cryptography aims to hide the meaning and content of the message, not its existence. Over the centuries, we have invented multiple techniques that allow us to do exactly that. In Julius Caesar's “Gallic Wars,', he described his method of encrypting communication to Cicero. This document is considered to be the first recorded use of a substitution (or shift) cipher for military purposes.
In the second half of the 16th century, Mary Stuart, who reigned over Scotland but was forced to abdicate in favor of her son, fled to England seeking the protection of her cousin Queen Elizabeth of England. Elizabeth took her in despite viewing her as a threat to her throne. Many years later, when a plot to assassinate Queen Elizabeth surfaced, the queen's investigators faced the challenge of proving what everyone thought -- that Mary was the chief conspirator. Mary was intelligent enough to take precautions in order to protect her communication, primarily with a group of English Catholics that supported her. Unfortunately for her, the cipher she used was not strong enough and was easily broken. Decrypting her messages and uncovering the muder plot eventually led to her beheading. From simple encryption techniques, such using a shift cipher, also known as a Ceasar cipher, we have moved to sophisticated, almost magical, algorithms created by the brightest minds of every contemporary era, each building on the latest advancements in the world of mathematics and computer science.
Whether it was Caesar or Mary Stuart, both had to agree with their interlocutors on a particular system to encrypt and decrypt messages. The set of rules they employed was the *key* to their communication. Up until the 1970s, every time someone wanted to send encrypted messages to the other party, it was necessary to encrypt them with a secret key. The problem with this key was that it either had to be agreed upon beforehand, or it needed to be delivered to the receiving party apart from the message itself. Even though the two usually were not sent through the same means, the sole existence of a key represented a point of attack. And it facilitated exploitation at every turn. History is rich with examples of leaked keys compromising important communications between parties, siphoned off to undesired hands. While cracking the intercepted messages caused Mary Stuart to lose her head, it meant wartime defeat for Nazi Germany. The survival of many nations, regimes, and peoples often rested entirely on the strength of the cipher.
As such, cryptography based on public-key infrastructure (PKI) represented a significant improvement in both security and reliability when it comes to encryption. Suddenly, there was no need to worry about securing communication channels for delivering the secret key. The newly-devised concept of key pairs has since become groundbreaking, setting in motion implications far beyond the imagination of its creators.
PKI is based on two types of keys, a public and a private one. It allows people to easily send encrypted pieces of information to anyone who knows their public key. The message, however, can only be decrypted by the holder of the private key corresponding to the public key. It is messaging made easy and secure. Some years later, this same technology allowed for the creation of pseudonymous networks such as Bitcoin and Ethereum, digital currencies.
Steven Levy’s famous book *“Crypto: How the Code Rebels Beat the Government - Saving Privacy in the Digital Age,”* is dedicated to the life and work of cryptography pioneers. It does a particularly good job narrating the story that brought Martin Hellman and Whitfield Diffie together to join forces protecting privacy on the Internet. And it is one hell of a story indeed.
Martin Hellman, a rather typical academic, working on his Ph.D. in “decision logic” achieved his first breakthrough with the release of his dissertation “*Learning with Finite Memor*y” in 1969. His further career led him to IBM in New York, working in the Pattern Recognition Department. While his work was not related to cryptography, he would occasionally socialize with his colleagues from the neighboring building, where one division of IBM focused on research in cryptography. Influenced by the time spent with his friend and colleague Horst Feistel, who David Chaum would later cite in his dissertation as “the father of modern conventional public cryptography,” he discovered the rabbit hole --- called cryptography --- which become an obsession for the rest of his career. Hellman spent a few years at MIT’s Department of Electronic Engineering, where he was mentored by another great cryptographer, Peter Elias. He returned to Stanford in 1971 to pursue his cryptographic research. However fascinated he was by the philosophical underpinnings of cryptography, he had little hopes of achieving something meaningful in the field dominated by well-funded government agencies that governed in secret. As he stated:
"How could I hope to discover anything that the National Security Agency, which is the primary American code-making, code-breaking agency, didn’t already know? And they classified everything so highly that if we came up with anything good, they’d classify it."
Nonetheless, he dug deeper and produced his first papers and lectures on the matter. Soon after, he met the person who would become his companion for years to come --- Whitefield Diffie.
Diffie began with an interest in cryptography in his childhood at the age of 10, wedded to his love of mathematics. After graduation, he began work as a software developer, working part-time at the Artificial Intelligence Laboratory at MIT with the man who would later become known as the father of artificial intelligence --- John McCarthy. From what we can tell, it was this inspiring working environment that greatly influenced Diffie. He would go on to follow McCarthy to Stanford, where he created a new AI Lab. During his tenure, he ran into another source of profound inspiration --- this time a book called “*The Codebreakers: The story of Secret Writing*” by David Khan. Diffie decided to pursue his own personal cryptographic research while driving around the country together with his wife, to meet and learn from different cryptography experts.
At some point, unsurprisingly, it was recommended that he pay Hellman a visit. In the first meeting, the two immediately fell into a fervent discussion that prolonged for hours. These encounters became more frequent and intense. They soon became friends and started to work together. By 1975, they had both turned to a common cause --- the Data Encryption Standard (DES). It was the first encryption ciphers approved for both public and commercial use. The sectors of business and finance then became keen adherents of this standard. This remains significant because prior to DES, cryptography was classified as a munition, or as a general military tool, and thus only licensed subjects could handle it in any form.
The idea to create a national standard for encryption came from the National Bureau of Standards, later renamed the National Institute of Standards and Technology (NIST). Research centers across the US were requested to submit design proposals to further study on the topic. In response, IBM created a cipher called *Lucifer*. The research activities at IBM that led to the final design of the cipher were led by the same man who had introduced Hellman to cryptography in the first place --- Horst Feistel.
The cipher’s research and design activities were conducted in close collaboration with NSA, which consistently advocated for reducing key sizes to better streamline their communicative protocols. Both Hillman and Diffie, to their credit, welcomed the involvement of the NSA, hoping it would serve as an important step towards more widespread public use of cryptography. It wasn’t long before rumors circulated among the research community that the cipher was tampered with by NSA. This deepened the general distrust surrounding government agencies that became prevalent in the period after WWII, thanks to the uncovering of the brutal tactics of totalitarian regimes. President Richard Nixon’s Watergate scandal, which eventually led to his resignation in 1974, amplified that perception. At that point, it became difficult to believe that the NSA would build a cipher without knowing how to crack it.
During that time, Ralph Merkle, an up-and-coming computer scientist from Berkeley, also became interested in cryptography. His research pondered the riddle of establishing secret communication between two parties and the probability it would be uncovered by an adversary. He tried to prove that it was mathematically impossible. But he failed, and again. Frustrated, he decided to tackle the riddle from the opposite direction --- to find ways to achieve it. He began working on his own cryptographic concepts that would turn out to be an early construction for public-key systems.
In an example scenario, Alice and Bob want to communicate, but there is an unwanted eavesdropper, named Eve, who has access to anything that the two exchange. Merkle and many before him had long wondered: how can Alice send a message to Bob that he can read and Eve can’t? Though it was thought of as impossible, Merkle solved it with an elegant solution.
Alice first creates puzzles which each contain an encrypted message. Each puzzle is challenging, yet feasible to be cracked by brute force. While it takes some effort to compute it, it is still solvable. So Alice creates, say, one million of these puzzles and sends them to Bob. Of course, Eve intercepts the message and has them all too. But what Bob does is choose one random puzzle and proceeds to solve it, cracking open the decrypted message. At this point, Alice and Bob have found a solution to this particular problem (Alice has all of them as she had created them). For Eve, it proves to be a challenge to decrypt all the puzzles, since she needs to perform a million such operations.
Now, Bob needs just to notify Alice which puzzle he has chosen. This can be easily done because the decrypted message contains an identifier along with a long digital key. He sends the message to Alice, and *eureka!* Now both have a shared key. Eve may, of course, continue cracking the puzzles one by one, but since there are so many, it will cost her much more in terms of computation power, time, and money to do so. This concept is called Merkle’s puzzle, as you may have been able to decipher. Merkle would later recall:
"Then I thought about it some more, and I said, “Well if I can’t prove that you can’t do it, I’ll turn around and try and figure out a method to do it.” And when I tried to come up with a method for doing it, having just tried to prove you can’t do it, I knew where the cracks in my proof were, so to speak, and I knew where I could try and slide through. So I worked on those places and lo and behold it turned out it was possible. I could use the cracks in my proof to come up with a method for actually doing it, and when I figured out how to do it, there was this, well, the traditional “aha moment” where I said, “Oh, yeah, that works. I can do it."

Source: Symmetric vs Asymmetric Encryption | Difference Explained
With no theoretical background or knowledge in cryptography, his work was so advanced that it was rejected by both his university professors as well as the computer science magazine where he submitted it. But his work did not go unnoticed entirely. It soon drew the attention of people close to Hellman and Diffie. Eventually, his work made it to the duo, who had recently published a paper exploring potential applications of public-key encryption. Reading Merkle’s work blew their minds. Merkle’s lack of cryptographic background was compensated by the immense creativity that purported to solve the problem of public key distribution that had bothered many academics for years. Combined with the in-depth cryptographic knowledge of Hellman and Diffie and Merkle’s initial idea, they improved it into a compact solution resulting in a new iteration of public-key cryptography. Soon they would formulate it in their paper: “*New Directions in Cryptography*”.
Even though the communication protocol was named *Diffie-Hellman key exchange*, when it was patented a year later in 1977, Merkle received his fair share of credit as one of the three inventors. The paper was a breakthrough, forever changing the status of the public’s access to powerful cryptographic technology. We can feel the spirit of rebellion at the end of their paper where they left this note:
"Inspire others to work in this fascinating area in which participation has been discouraged in the recent past by a nearly total government monopoly"
Just a few months later, in 1977, the concept was improved by a trio whose initials would become known to anybody in the field of mathematics and cryptography. Ron Rivest, Adi Shamir, and Leonard Adleman, all at MIT at the time, focused their work on designing a one-way function. This function would be easy to calculate in one direction but would be computationally infeasible to invert. They invented an algorithm called *RSA*, which based its asymmetry on the practical difficulty of the factorization of two large numbers. Even though they were asked not to publish it by intelligence services, they ignored them and did so anyway. While the algorithm was considered relatively slow, it was still mostly used for encryption of shared keys for symmetric key cryptography, rather than for encryption and decryption of data. From then on, RSA became used widely as an algorithm of choice for secure data transmission.
The RSA algorithm could also be used to produce digital signatures. This modified version became widely used in mainstream software for the first time in Lotus Notes in 1989. After RSA, other digital signature schemes were developed by Lamport, Rabin, and Merkle.
It is worth noting that, as revealed later, the aforementioned researchers were not the first to conceive cryptography based on PKI, as it was partially created and applied by intelligence services in Great Britain. English mathematician Clifford Cocks developed an equivalent system around 1973, but his work was classified as top secret and would not be publicly revealed until the late 1990s. Nonetheless, intelligence agencies, including the NSA, had access to these valuable sources, but they remained classified. Thankfully, there were plenty of fervent mavericks and cryptography enthusiasts working for the good of the public.

Source: Symmetric vs Asymmetric Encryption | Difference Explained
Hash Functions & Merkle Trees
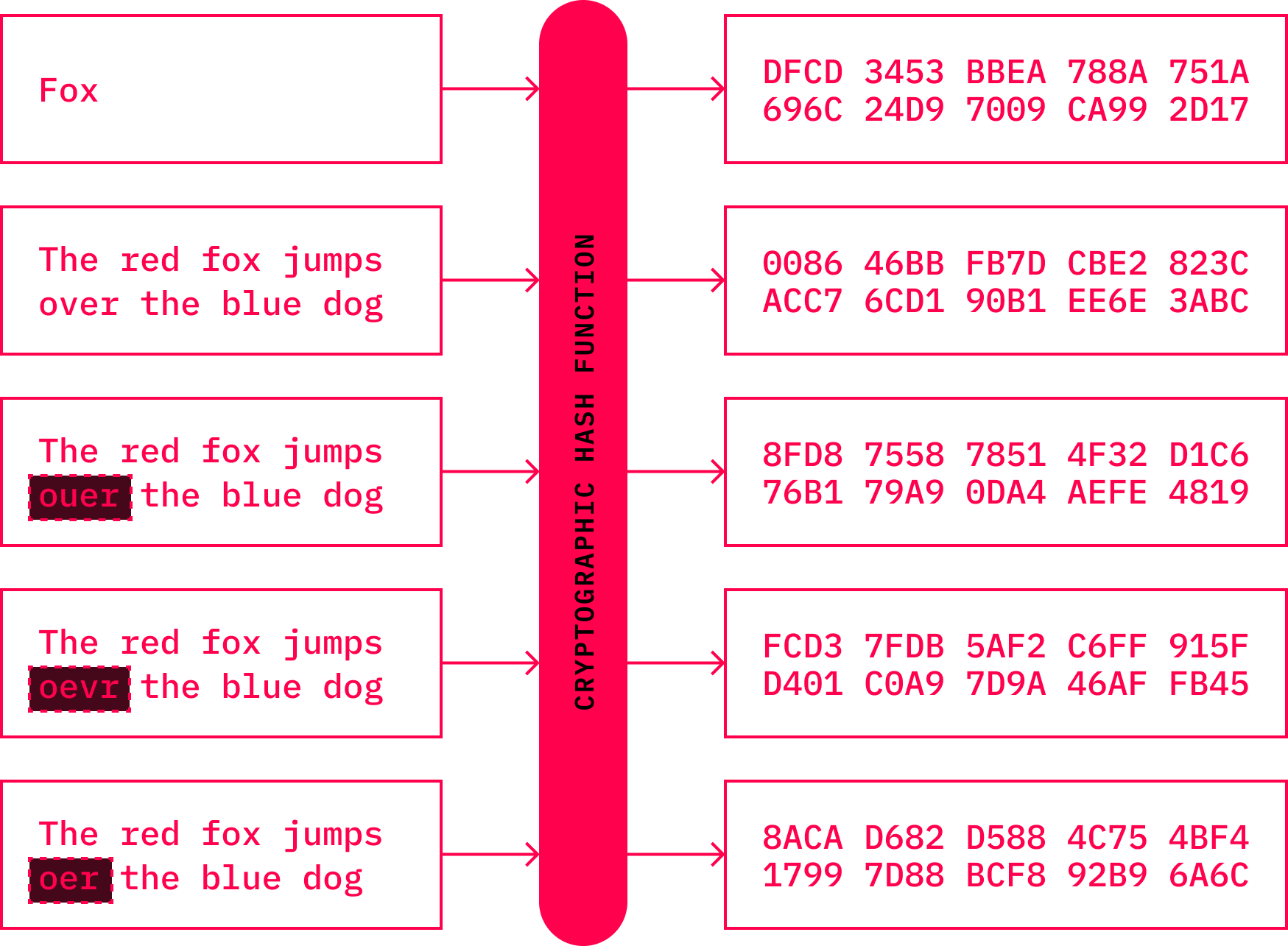
Hash functions have been notoriously referred to as the “Swiss army knives” of cryptography. They have become one of the most fundamental tools and weapons in the Internet’s stack. A hash function maps data inputs of arbitrary length to short outputs in the form of a short string of data of fixed length. These were called one-way functions, as it is easy to compute the output from the input, but it is extremely hard to reverse the process. This allowed for easy verification of whether data has been corrupted or sabotaged. With that in mind, hash functions are very useful for identifying datasets. It is also helpful when looking for duplicates within large datasets. The need for such a technique was described by Diffie and Hellman in their seminal paperThe first proposals emerged soon thereafter. Many more designs were created in the 1980s, and by the mid-1990s, about a few dozen hash functions were known. Since then, hundreds of different functions have been proposed. Bitcoin utilizes several such functions, SHA-256 and RIPEMD-160, to name a few, while other cryptocurrencies embraced different hash functions.
Source: Hash Function | Wikipedia
There are several key properties desired in hash functions:
- Applying the hash function *f* on input *A*, should always result in the same output *A’*. Therefore: *f(A) = A’*
- They should be resistant to collisions, which means that no two data inputs should result in the same output value.
- Knowing the hash value would make it difficult to reasonably restore the initial data input --- also known as preimage --- in any short period of time
- Furthermore, even the knowledge of the preimage, together with its hash value, would not let anyone create a preimage with the same output.
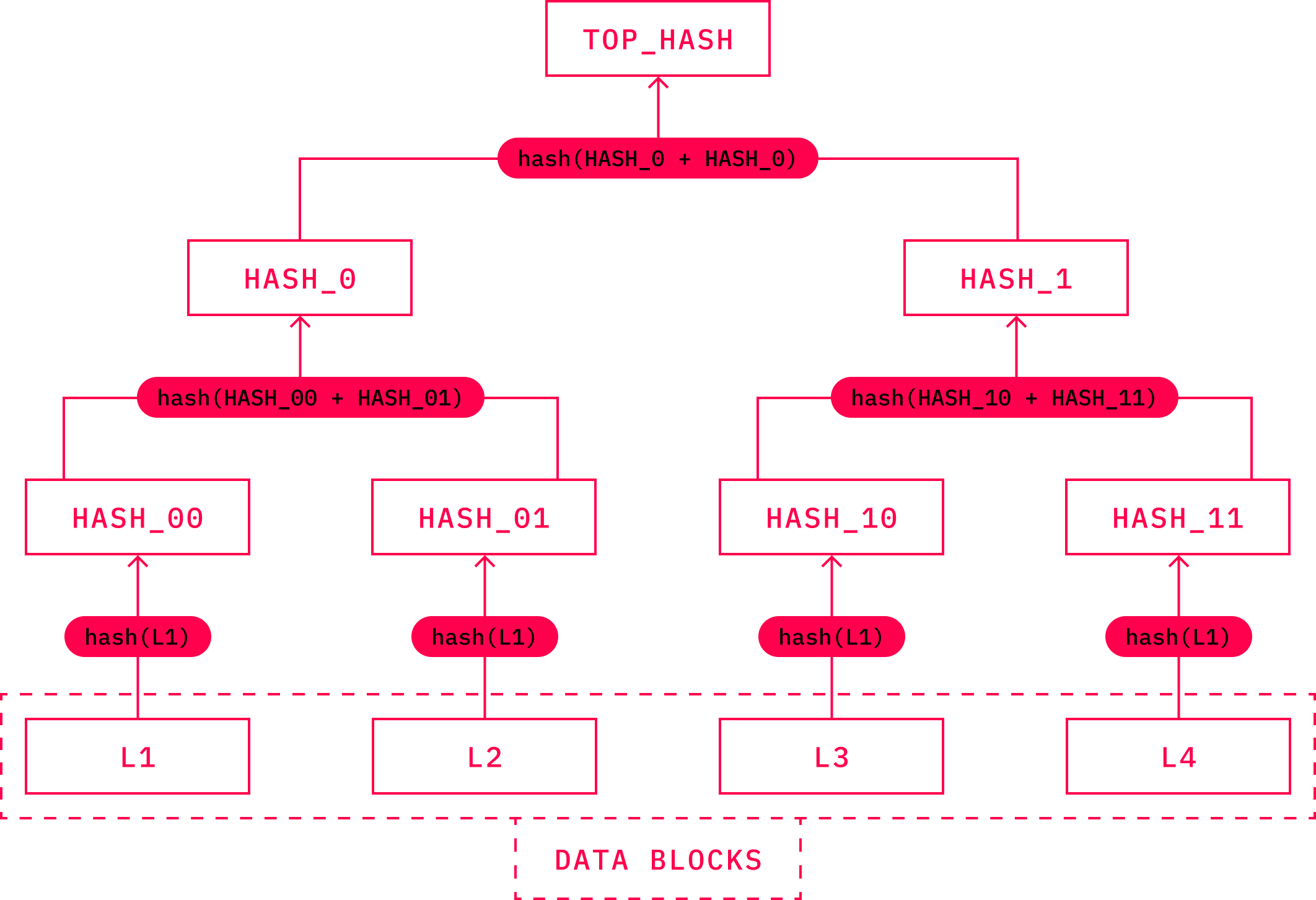
Another important component of the cryptographic toolset, found not only in cryptocurrencies, is a data structure called Merkle Tree. Merkle Trees are specific data structures that link separate pieces of data with a single root hash value. They typically consist of three rudimentary components, such as leaves, nodes, and roots. Merkle leaves are hash values produced by datasets. Hashing two of such leaves results in a Merkle node. Visualizing this, we can create a pyramid-like structure with the Merkle root on top. This principle is also used when storing transactions within the Bitcoin blocks.
Source: Merkle Trees | Wikipedia
The Byzantine Generals Problem
In parallel to the efforts leading to the inception of asymmetric encryption techniques, another emerging field of research added to the field of cryptography. The early 1980s marked the introduction of Usenet --- a Unix-based network that allowed for the creation of bulletin boards and discussion forums that eventually turned into a massive social platform. The adoption of the TCP/IP standard by Arpanet opened the network to the world, introducing communication compatibility between a much broader range of computer hardware. With the gradual evolution of computer systems, it was the first indication that the future would soon bring and utilize methods to deploy *distributed computing.* In distributed systems, multiple components located on different networked computers interact with each other to achieve a common goal.
Perhaps the earliest example of a large-scale application using distributed computing was email on the Arpanet, established by the Advanced Research Projects Agency (ARPA). Much later, a “D” was added to its name for “Defense,” underlining the importance of the agency's activities for national security. As the applications evolved into more complex systems, the need to design schemes that provided a certain level of resilience or tolerance to system failures became necessary. Distributed (also known as concurrent or parallel) computing later became its own branch of computer science focused on problems such as state replication. The field is inescapably associated with the work of Leslie Lamport, a Turing-awarded computer scientist who contributed significantly to the development of fault-tolerant distributed systems.
"A reliable computer system must be able to cope with the failure of one or more of its components. A failed component may exhibit a type of behavior that is often overlooked--namely, sending conflicting information to different parts of the system. The problem of coping with this type of failure is expressed abstractly as the Byzantine Generals Problem."
Lamport and his co-authors --- Robert Shostak and Marshall Pease --- introduced their seminal paper from 1982 with the paragraph above. It has since become one of the most cited papers in the field, named after the analogy they draw upon in the paper: the Byzantine Generals Problem. The paper describes several divisions of the Byzantine army that camp around an enemy city. The generals are able to communicate with one another only by messengers. As they observe the enemy, they need to reach an agreement on what would be the best time to attack. Once they decide on that time, they need to attack in coordination. Failure to do so would lead to their defeat.
What they needed was to find an algorithm that would guarantee that all loyal generals would decide upon the same action plan and that a small number of traitors couldn’t push the loyal generals to adopt a bad strategy. The problem, while formalized in this paper, was earlier conceived of by Shostak, who dubbed it an *interactive consistency problem*.
The trio also presented multiple possible solutions they had designed, later improved on either by them or others in the years that followed. This includes the *Paxos* protocol, published for the first time in 1989, and the *Practical Byzantine Fault Tolerance* algorithm published in 1999 by Miguel Castro and another Turing award-winning scientist Barbara Liskov. A breakthrough in this field came with the revelation of the *Nakamoto consensus* implemented in Bitcoin. As was common, a lot of preceding work on this topic operated with an assumption of a set of nodes (or quorum) that were known to each other. Nakamoto managed to compile many of the technologies that had been discovered decades earlier in a unique way that allowed for a peer-to-peer network to be operational with (tens of) thousands of anonymous nodes joining and leaving the network at any time. The utilization of the Proof-of-Work algorithm for a network’s consensus has become arguably controversial (not so much within the Bitcoin community as elsewhere) as far as its efficiency is concerned, yet doubtlessly effective. We get more into details of PoW in the next chapters, and we discuss its potential alternatives in chapter seven. The emergence of Bitcoin sparked an industry-wide interest in research of consensus algorithms, many of which are covered in chapter five.
Elliptic Curve Cryptography
In 1985, another crucial piece of the puzzle of cryptographic primitives that would later become foundational for the cryptocurrency came onto the scene. Neal Koblitz and Victor Miller independently proposed cryptographic techniques based on elliptic curves. They were inspired by H.W. Lenstra, who came up with the first elliptic curve factoring algorithm. Elliptic curve cryptography (ECC) is an approach to PKI based on the algebraic structure of elliptic curves over finite fields. In cryptocurrencies, elliptic curves are mainly applicable for digital signature schemes, and pseudo-random generators. Bitcoin, for instance, adopted the Secp256k1 elliptic curve which simply refers to certain parameters used when generating the key pairs. This particular elliptic was not widely used before Bitcoin became popular, but gained traction afterward due to its several nice properties.
ECC brought many advantages over typical integer factorization that were attractive for security applications. It allowed smaller key sizes or bandwidth savings that eventually resulted in faster implementations, but it took some time before the concept gained trust in the industry. In the early 21st century, ECC then became one of the most widely used and trusted cryptography techniques. Elliptic curves entered wide use around 2005 when the NSA published their paper titled “*The Case for Elliptic Curve Cryptography*” with the following comments:
"The best assured group of new public key techniques is built on the arithmetic of elliptic curves. This paper will outline a case for moving to elliptic curves as a foundation for future Internet security. This case will be based on both the relative security offered by elliptic curves... and the relative performance of these algorithms. While at current security levels elliptic curves do not offer significant benefits over existing public key algorithms, as one scales security upwards over time to meet the evolving threat posed by eavesdroppers and hackers with access to greater computing resources, elliptic curves begin to offer dramatic savings over the old, first-generation techniques."
In an interesting twist, a decade later the NSA released another paper with a negative outlook on ECC. The paper suggested that since the threat of quantum computing is so close, those who had not yet upgraded to ECC from RSA should not even bother to do so, and should instead focus on improving post-quantum protocols. Such a recommendation surprised the cryptographic community, including the greats such as Schneier and Koblitz, as it was widely believed it would be used for another decade or two. Regardless, in 2021 ECC systems remain to be widely used across the industry.
Birth Of Digital Anonymity
When we trace back the origins of the first attempts to design digital currencies, we inevitably run into American computer scientist and cryptographer David Chaum. Similar to Ralph Merkle, Chaum went to the University of California, Berkeley. In the late 1970s, the Bay Area was a great place to be. The personal computer revolution was picking up steam. *Hewlett Packard* had already been a force for a few decades, having been recognized as the symbolic founder of Silicon Valley. At the same time, *Intel* had been experiencing rapid expansion and growth of their business. And “the two Steves” --- Jobs and Wozniak --- had just incorporated *Apple Computer, Inc.*, while working on their “*Apple II*” machine.
It was as if the world was introduced to the Jedi Order and the story of Luke Skywalker becoming the guardian of peace and justice in the galaxy. Excitement and fascination by technology’s potential had been spreading, and digital frontiers had been rapidly expanding. Outside the Bay area, Microsoft was closing its second year of operations with revenue of just over $16,000. The ARPANET was recently (since 1975) declared “operational”, and its network already consisted of a few dozens of nodes known as IMPs (Interface Message Processors) while adding new nodes every few months. The expectations from the technology industry culminated throughout 1980 as the market anticipated the biggest IPO of its day. The computer company from Cupertino was a hot commodity, as The Wall Street Journal wrote shortly before Apple’s public offering:
"Not since Eve has an Apple posed such temptation"
There was a fascinating scene unfolding, with the public key cryptography advancing in the background, stimulating the imagination and geekery of the technology pioneers. Chaum, from a well-positioned family, had access to computer systems early in his childhood. As a student of cryptography, he was spending time playing around, learning to crack passwords and break them. Chaum developed great instincts on most technologies and realized there was something that general discourse on cryptography tended to overlook: problems related to metadata. Even though the content of messages could be encrypted, the traffic analysis alone could potentially reveal a great deal of valuable information, such as who has a conversation with whom and when. That posed a significant risk of compromising one’s privacy. Indeed, decades later, he would be proven right as traffic analysis represented a real threat not just in cryptocurrencies such as Bitcoin but the Internet itself.
Chaum dug deeper into the traffic analysis problem, and in 1979 released his first major paper in the field of cryptography: “*Untraceable Electronic Mail, Return Addresses, and Digital Signatures*”. Here’s part of the abstract:
"A technique based on public key cryptography is presented that allows an electronic mail system to hide who a participant communicates with as well as the content of the communication--in spite of an unsecured underlying telecommunication system. The technique does not require a universally trusted authority. One correspondent can remain anonymous to a second while allowing the second to respond via an untraceable return address."
Merkle, Diffie, and Hellman were, of course, cited, as well as other masterminds of that age: David Kahn, Paul Baran (the inventor of packet-switching), and the famous trio Rivest, Shamir, and Adleman. The paper sketched out an anonymous mailing protocol utilizing a *Mix Network,* where the identity of the messengers would be protected. Mix Networks --- or Mixnets --- consisted of nodes that would send information among each other to mix up the identity of the original sender and timing of the messages. PKI would be used for message authentication. A message would be encrypted and passed to a node where it would bundle with other messages from different senders. Then, it would bounce between different nodes, and exit the network at the destination address, while not revealing the original sender. Such a mixing protocol would later inspire the inception of Tor -- the anonymous browser that lets you access the deep (also known as dark) web.
Chaum foresaw that traffic analysis would sooner or later prove problematic not only for sending messages, but payments as well. This was at the time when Michael Aldrich had demonstrated the first online shopping system by connecting a modified domestic TV to a real-time transaction processing computer via a domestic telephone line. It was installed in a Tesco store in the UK. Hardly anybody could have predicted the buzz and hype *e-commerce* would cause a few decades later. But John Markoff saw this somewhat in the 1970s, as he in his book “*What the Dormouse Said: How the Sixties Counterculture Shaped the Personal Computer Industry”:*
"In 1971 or 1972, Stanford students using Arpanet accounts at Stanford University's Artificial Intelligence Laboratory engaged in a commercial transaction with their counterparts at Massachusetts Institute of Technology. Before Amazon, before eBay, the seminal act of e-commerce was a drug deal. The students used the network to quietly arrange the sale of an undetermined amount of marijuana."
Oddly enough, the cannabis sale would later achieve fame as the first-ever e-commerce transaction. It is worth noting that the transaction happened more than three years before the ARPANET was considered operational, however. Nonetheless, in 1982, Chaum published a legendary paper called “*Blind signatures for untraceable payments,*” wherein he proposed the idea of digital cash for the first time. The paper’s summary reads:
"A new kind of cryptography, blind signatures, has been introduced. It allows realization of untraceable payments systems which offer improved audibility and control compared to current systems, while at the same time offering increased personal privacy."
The system was designed to work within the banking infrastructure, and therefore would rely on a central entity but would provide the transacting parties with an unprecedented level of privacy as the protocol masked the sender, the amount being transacted, and also the time when the transaction occurred. His work did not get much attention from his peers, and was deemed rather radical at the time. Despite that, he did not get discouraged. Instead, he proceeded with his research and received a Ph.D. with his dissertation “*Computer Systems Established, Maintained and Trusted by Mutually Suspicious Groups,”* where he elaborated on systems that don’t trust each other, and argued for the need for decentralized services. Decentralization, along with cryptography, was meant to achieve the ultimate goal --- to protect personal privacy. All of his work revolved around this goal. Chaum would evangelize on the topic further in his other paper “*Security without Identification: Card Computers to make Big Brother Obsolete,”* where he brought up the fact that privacy threats would be omnipresent in an ever-more interconnected world:
"Computerization is robbing individuals of the ability to monitor and control the ways information about them is used. Already, public and private sector organizations acquire extensive personal information and exchange it amongst themselves. Individuals have no way of knowing if this information is inaccurate, outdated, or otherwise inappropriate, and may only find out when they are accused falsely or denied access to services. New and more serious dangers derive from computerized pattern recognition techniques: even a small group using these and tapping into data gathered in everyday consumer transactions could secretly conduct mass surveillance, inferring individuals' lifestyles, activities, and associations. The automation of payment and other consumer transactions is expanding these dangers to an unprecedented extent."
Chaum was aware of the gravity of the situation as he understood the Internet’s design and saw the direction its architecture, and the world, was going in. He foresaw that decentralized architectures, supported by secure cryptography and the laws of mathematics, would be the only ways one would be able to retain sovereignty in the increasingly digital world. He conveyed his warning by referring to the famous Orwell’s dystopian novel *1984* in the paper’s title. Over thirty years after the publication of his writings, with untold numbers of data leakage scandals making headlines, it seems we didn’t listen.